Spændingsfald – Beregning, formler og eksempler

Hjem
>>
Dimensionering
>>
Spændingsfald – Beregning, formler og eksempler

Skaber spændingsfaldsberegning problemer, eller mangler du blot at få opsummeret teorien? Så er du havnet det rigtige sted. Jeg vil i dette indlæg beskrive og forklare teorien for spændingsfald. Du kan samtidig finde formler og eksempler på beregning af spændingsfald.

Indlægget vil komme ind på spændingsfald ved jævnstrømskredse, 1-faset vekselstrømskredse og 3-faset vekselstrømskredse. Anvend eventuelt indholdsfortegnelsen til højre for at navigere rundt på siden.

Hvad er spændingsfald

Spændingsfald er kort fortalt forskellen mellem den påtrykte spænding og spænding ved forbrugeren. Spændingsfaldet opstår, da alle passive kompoenter (Kabler, ledninger og udstyr) har en impedans. De er en del af en serieforbindelse, og derved vil de skabe en del af kredsløbets samlede spændingsfald. Samtidig ved et spændingsfald også resultere i et effekttab, der er rent spild.

Udover effekttabet, kan en for lav spænding ved forbrugeren resultere i, at forbrugeren ikke kører efter hensigten. Det er derfor mange gode grunde til at sikre, at spændingsfaldet er minimeret.
Spændingsfaldet afhænger af de passive komponenters impedans/modstand, og den samlede strøm i kredsløbet. Dette kan forklares ud fra Ohms lov.

$U=I*R$

En større strøm = større spænding og en større modstand = større spænding.

Spændingsfald definition

Definationen på spændingsfaldet er forskellen mellem forsyningsspænding og spændingen ved brugsgenstanden.

Spændingsfald formler – Generelle

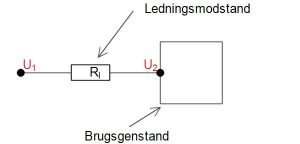
For at beregne på spændingsfald, skal vi først have begreberne på plads. Vi anvender beregrebet $U_1$ om spændingen i forsyningspunktet, og begrebet $U_2$ om spændingen ved forbrugeren. Den numeriske forskel på de to spændinger er vores spændingsfald . Derudover angives ledningsmodstand, ledningsinduktans og ledningsimpedans som $R_l$ , $X_l$ og $Z_l$ . Dog skal du først kun koncentrerer dig om ledningsmodstanden.

Ledningsmodstand

Til beregning af spændingsfaldet er det vigtig at kende ledningsmodstanden. Der er generelt to måder, hvorpå man kan finde ledningsmodstanden. Enten findes den i et kabelkatalog, eller beregnes den.
Beregning af ledningsmodstanden gøres ved anvendes af lederen resistivitet efter formlen:

$R_l=\varrho*\frac{l}{S} [ \Omega]$

Begreberne betyder følgende:

$\begin{align*} & R_l=Ledningsmodstand \ [ \Omega] \\ & \varrho=Lederens resistivitet \ [ \frac{\ Omega*mm^2}{m}] \\ & l=l\ae ngde \ [m] \\ & S=Lederens tværsnit \ [mm^2] \end{align*}$

Beregnes spændingsfald ved jævnstrøm og 1- og 2-faset vekselsstrøm, skal kablets længde gangen med 2, da du har et spændingsfald i ledningen retur til forsyningspunktet. Det er ikke gældende ved 3-faset vekselsstrøm grundet teorien bag 3-faset.

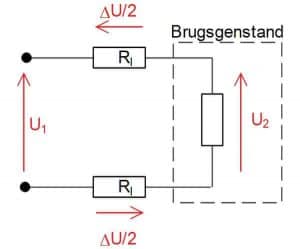
Hvordan spændingsfaldet agere er illustreret i figur 2, hvor der modstand i begge leder – eksempelvis i fase og nul.
Lederens resistivitet er materiale afhængig, hvor kobber og aluminium anvendes oftest.

$\begin{align*} & \varrho_{cu}=0,01724 \ [ \frac{\Omega*mm^2}{m} ] \\ & \varrho_{alu}=0,02826 \ [ \frac{\Omega*mm^2}{m} ] \end{align*}$

Når man skal finde sin ledningsmodstand anvendes ofte kabelkataloger, hvor ledningsmodstanden er opgivet i Ohm pr. kilometer. Derved kan kablets ledningsmodstand beregnes efter følgende formel.

$R_l=\frac{r_l}{1000}*l \ [\frac{\Omega}{km}]$

Lille $r_l$ anvendes i dette indlæg om ledningsmodstand opgivet i kataloger – altså ikke omregnede ledningsmodatande.
Ledningsmodstanden vi enten beregner eller finder i kabelkataloger er angivet ved 20 grader. Da modstanden er afhængig af temperatur, skal du tage højde for det, hvis du arbejder ved andre temperatur end 20 grader.

Ledningsmodstand ændring ved temperaturforskelle

For at beregne ledningsmodstand ved andre temperatur end 20 grader anvendes følgende formel:

$R_T=R_l*(1+\alpha*(T-20)) \ [ \Omega]$

Her indsættes den beregnede ledningsmodstand ved 20 grader, $alpha$ er 0,004 $[C^{-1}]$ (Værdien for kobber og Alu), og er en temperaturkoefficient. T er temperatur i grader.

Eksempel

Et kablet forsyner en brugsgenstand. Kablet er et 1,5 mm2 3-leder kabel med jord. Kablets længde er 10 meter og af kobber. Beregn kablets ledningsmodstand.

$\begin{align*} &R_L=\varrho*\frac{l}{S} \\ &R_L=0,01724* \frac{2*10}{1,5}=0,230 \ [ \Omega] \end{align*}$

Kablet føres ved en temperatur på på 40 grader. Beregn modstanden nu:

$\begin{align*} &R_T=R_l*(1+\alpha*(T-20)) \\ &R_T=0,230*(1+0,004*(40-20)) \\ &R_T=0,248 \ [ \Omega] \end{align*}$

Beregning af spændingsfald

For at beregne spændingsfaldet i kredsløbet, anvendes Ohms lov. Derfor skal du kende brugsgenstanden strøm og ledningsmodstanden.

$\Delta U=I_B*R_L$

Herefter kan spændingen i forsyningspunktet $U_2$ beregnes på denne måde:

$U_2=U_1-\Delta U$

Denne formel kan anvendes ved beregne af jævnstrøms kredsløb. Ved beregning af 1-faset og 3-faset vekselsstrøms kredsløb, er formlerne en smule udvidet. Dette forklares senere i dette indlæg.

Spændingsfald i procnet

Når man snakker spændingsfald, er det ofte i procent. Derfor kræver det også at beregningerne er i %. Til beregning af den procentvise spændingsfald anvendes formlen:

$\Delta U_{\%}=\frac{\Delta U}{U}*100$

Effekttab

Grundet modstanden i kablet, vil der ske et effekttab. Denne kan beregnes med følgende formel:

$P_{tab}=\Delta U*I_B=\frac{\Delta U^2}{R_L}=I^2*R_L$

Spændingsfald ved jævnstrøm

Den mest simple måde at beregne spændingsfald er ved jævnstrø. Her skal der ikke tages højde for hverken den induktive eller kapacitive indvirkning på kablerne – og derved er der kun den resistive modstand, der har indvirkning på spændingsfaldet.

Derved er fremgangsmåde:

Beregn ledningsmodstand
Beregn forbrugerens strøm
Beregn spændingsfaldet

Før i dette indlæg blev formlerne for beregning af ledningsmodstand forklaret, og vi kom frem til følgende:

$\begin{align*} &R_l=\varrho*\frac{l}{S} [\ \Omega] \\ &R_T=R_l*(1+\alpha*(T-20)) \ [ \Omega] \end{align*}$

Har vi ikke i forvejen fået forbrugerens strøm opgivet, har vi ofte en effekt og en spænding opgivet. Da vi med stor sandsynlighed ikke kender spændingen ved forbrugeren, bliver det en tilnærmet beregning af strømmen. Dog vil der ved anvendelse af denne strøm altid sikre dig mod “Worst Case”. Derved kan strømmen beregnes på en af følgende måder:

$I_B=\frac{P}{U}=\frac{U}{R}=\sqrt{\frac{P}{R}} \ [A]$

Herefter kan spændingsfaldet beregnes.

$\Delta U=I_B*R_l$

$\Delta U_{\%}=\frac{\Delta U}{U}*100$

Eksempler på beregning af spændingsfald ved DC

Eksempel 1: I et 20V jævnstrømskredsløb, er der anvendt et 25 meter langt kabel til em lampe. Lampen har et forbrug på 2 ampere. Der er anvendt 1,5 mm2 ledning. Beregn spændingen ved brugsgenstanden og den procentmæssige spændignsfald. Der skal ikke tages højde for temperatur.

$\begin{align*} &R_l=\varrho*\frac{l}{S}=0,01724*\frac{25*2}{1,5}=0,575 \ [ \Omega] \\ &\Delta U=I_B*R_l=2*0,575=1,149 \ [V] \\ &U_2=U_1-\Delta U=20-1,149=18,851 \ [V] \\ &\Delta U_{\%}=\frac{\Delta U}{U_1}*100=\frac{1,149}{20}*100 = 5,75 \ [\%] \end{align*}$

Der er derved et stort spændingsfald

Eksempel 2: I en jævnstrøms kredsløb er der anvendt en 12-24 volt horn (Ren ohmsk). Hornet er tilsluttet 12 V, og anvender 1,2 ampere ved drift. Den er forsynet med en 0,75 mm2 kabel, som har en længde på 10 meter. Beregn spændingen ved hornet.

$\begin{align*} &R_l=\varrho*\frac{l}{S}=0,01724*\frac{10*2}{0,75}=0,460 \ [ \Omega] \\ &\Delta U=I_B*R_l=1,2*0,460=0,552 \ [V] \\ &U_2=U_1-\Delta U=12-0,552=11,448 \ [V] \\ &\Delta U_{\%}=\frac{\Delta U}{U_1}*100=\frac{0,552}{12}*100 = 4,60 \ [\%] \end{align*}$

Hornet forsynes nu med 24V, beregn nu, hvad spændingen er ved hornet, hvis det antages, at den yder samme effekt?

$\begin{align*} &P_h=U_1*I_B=12*1,2=14,4 \ [W] \\ &I_{ny}=\frac{P_h}{U_{1-ny}}=\frac{14,4}{24}=0,6 \ [A] \\ &\Delta U_{ny}=I_ny*R_l=0,6*0,460=0,276 \ [V] \\ &U_{2-ny}=U_{1-ny}-\Delta U_{ny}=24-0,276=23,724 \ [V] \\ &\Delta U_{\%-ny}=\frac{Delta U_{ny}}{U_{1-ny}}*100=\frac{0,276}{24}*100 = 1,15 \ [\%] \end{align*}$

Spændingsfald ved 1- og 2-faset vekselsstrøm

Skal du beregne spændingsfald på et 1-faset vekselsstrømskreds, er det er smule anderledes, sammenlignet med jævnstrøm. I vekselstrøm kan der opstå induktive og kapacitive belastning, samt der tilføres et induktiv reaktans i kablet. Derved opstår en $X_l$ , som skal medregnes. Normaltvis er denne $X_l$ meget lille kabler under 50 $mm^2$ . Derfor ses der ofte bort fra denne ved mindre kabler.

Til beregning af spændingsfald ved vekselstrøm, kan der anvendes forskellige fremgangsmåder. Jeg vil beskrive en tilnærmet resultat. Derudover kan man beregne sig til et præcis resultat. Forskellen er ofte meget lille, derfor anvendes ofte en tilnærmet resultat.

Formler – Tilnærmet resultat

Til beregning af spændingsfald i 1-faset vekselstrømkredsløb, anvendes følgende formel:

$\Delta U=I_B*(R_l*cos\varphi_B+X_l*sin\varphi_B)$

Anvendes overstående formel, kan $X_L$ -ledet undlades ved en ren ohmsk belastning, da sinus til 1 = 0. Derved udgår $X_l$ . Beregnes der på en induktiv belastning, kan overstående formel anvendes i fulde udstrækning. Beregnes der på en kapacitiv belastning, skal fortegnet i parentesen ændres til modsat fortegn.

Derved:

$\begin{align*} &\Delta U=I_B*R_l*cos\varphi_B \ (Resistiv belastning) \\ &\Delta U=I_B*(R_l*cos\varphi_B+X_l*sin\varphi_B) \ (Induktiv belastning) \\ &\Delta U=I_B*(R_l*cos\varphi_B-X_l*sin\varphi_B) \ (Kapacitib belastning) \end{align*}$

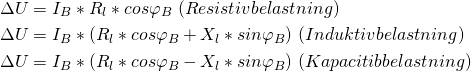
Formlen giver ikke et 100% korrekt resultat. Dog anses det, at når der udarbejdes spændingsfalds beregninger, er der mange fejlkilder. Der kan blandt andet nævnes:

Belastningstrømmen
Forsyningsspænding
Faseforskydning

Derfor accepteres overstående formel ofte, da fejlkilden er meget lille i forhold til. Jeg vil vise eksempler senere i indlægget på beregning af spændingsfaldet.

Formler – Præcis resultat

For at beregne en mere præcis resultat, skal vi først have styr på vektordiagrammerne ved resistiv, induktiv og kapacitiv belastning.

Vektordiagram for spændingsfald

Et kabel består elektrisk af en resistans og en induktans, hvilket har indvirkning på spændingsfaldet.
For at beregne impedansen af kablet, skal kablets resistans og induktans lægges sammen. Da de er i serie, er det efter reglerne for serieforbindelser.

$\begin{align*} &\vec Z_l=\vec R_l+\vec X_l \\ &Z_l=\sqrt{R_l^2+X_L^2} \end{align*}$

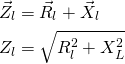
Resistive belastning

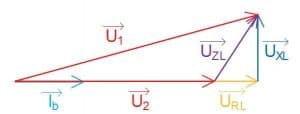
Figur 6: Vektor AC 1-faset Resistiv belastning spændingsfald

En resistiv belastning (Ohmsk), har ingen faseforskydning mellem strøm og spænding. Beregnes der på spændingsfald, anvendes spændingen ved forbrugeren som vores reference. Vektoren for spænding ved forbrugeren er derved placeret i 0 grader.

For at tegne et vektordiagram over spændingerne i et ren ohmsk belastning, skal vi først have fastlagt vores strøm. Vektordiagrammet vises på figur 6. Da der i en resistiv belastning ikke er faseforskydning mellem strøm og spænding, vil belastningstrømmen $I_B$ ligge i 0 grader ligesom spændingen ved forbrugeren (Den blå pil). Tages den resistive spændingsfald (Orange pil) over kablet, vil den ligge i fase med strømmen. Den vil derfor ligge i forlængelse spændingen ved forbrugeren. Dette er illustreret ved den gule pil på Figur 6. Da den induktive spænding er 90 grader foran strømmen, vil den derfor være placeret med 90 grader på resistansen. Det er illustreret ved den mørkeblå pil. Den lilla pil illustrer impedansens spændingsfaldet, der er resultatet af den resistive og induktive spændingsfald ved vektoriel beregning.

Den samlede spændingsfald kunne så fristes til at være $U_{ZL}$ , hvilket dog ikke er tilfældet. En spændingsfald er den nummeriske resultat af forsyningsspænding og spænding ved forbrugeren. Derfor skal $U_1$ beregnes, hvorefter spændingsfaldet beregnes. Dette kan gøres vektorielt eller ved hjælp af trekantsregler. Jeg vil dog udelukkende forklare de vektorielle beregninger.

Induktive belastning

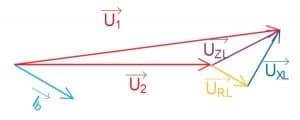
Figur 8: Vektor AC 1-faset Induktiv belastning spændingsfald

Ved induktiv faseforskydning forskydes vektorerne for spændingsfaldene. Strømmen er tegnet ved den blå pil, og er forskudt bagud i forhold til vektorerne. Da den resistive del er 0 grader forskudt i forhold til belastningstrømmen, vil den resistive spændingsfald ligge parallel med belastningsstrømmen. Dette er illustreret ved den gule pil på figur 8. Igen vil kablets induktive spændingsfald ligge 90 grader foran strømmen, og derved vinkelret på den resistive spændingsfald. Dette illustreres ved den mørkeblå pil.

Grundet de vektorielle beregninger er formlerne ens i forhold til beregning af den resistive belastning:

Kapacitive belastning

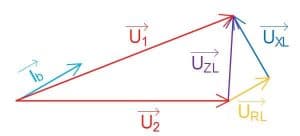
Figur 9: Vektor AC 1-faset Kapacitiv belastning spændingsfald

Ved kapacitiv belastning er strømmen foran spænding, og er derved foran spænding ved forbrugeren. Den vises ved den blå pil $I_B$ på figur 9. Den resistive spændingsfald ligge parallel med strømmen, hvilket er illustreret med den gule pil på figur 10. Igen vil den induktive del være 90 grader foran strømmen og derved. Ved en kapacitiv belastning kan det risikeres, at forsyningsspænding er lavere end forbrugerspændingen. Dette skyldtes, at vektorerne peger “bag ud”.

Formler for spændingsfald

Spænding $U_1$

$\begin{align*} &\vec U_1=\vec U_2+\vec I*\vec R_L+\vec I*\vec X_L \\ &\vec U_1=\vec U_2+\vec I*\vec Z_L \\ &\vec U_1=\vec U_2+\vec I*(\vec R_l+\vec X_l) \\ \end{align*}$

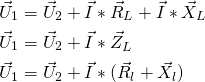
Spændingsfaldet $\Delta U$

$\begin{align*} &\Delta U=U_1-U_2 \end{align*}$

Eksempler på beregninger

Eksempel 1: En forbrugsgenstand har en belastning på 10 ampere med en $cos\phi=0,8 \ (Induktiv)$ . Der er målt en spænding på 230V ved brugsgenstanden. Der er anvendt et 20 m langt kabel med en reaktans på $1,013 \ [\frac{\Omega}{km}]$ og en resistans på $12,1 \ [\frac{\Omega}{km}]$ . Tegn et vektordiagram og beregn den påtrykte spænding.

Beregning af $R_l$ og $X_l$ .

$\begin{align*} &R_l=\frac{r_l*l*2}{1000}=\frac{12,1*20*2}{1000}=0,484 \ [\Omega] \\ &X_l=\frac{x_l*l*2}{1000}=\frac{1,013*20*2}{1000}=0,041 \ [\Omega] \end{align}$

Faseforskydningsvinklen beregnes

$\angle \phi_b=cos^{-1}(0,8)=-36,87 [^{\circ}]$

Tilnærmet beregninger

$\begin{align*} &\Delta U=I_B*(R_l*cos\varphi_B+X_l*sin\varphi_B) \\ &\Delta U=10*(0,484*cos(36,87)+0,041*sin(36,87) \\ &\Delta U=4,12 \ [V] \end{align*}$

Præcis beregning

$\begin{align*} &\vec U_1=\vec U_2+\vec I*\vec R_L+\vec I*\vec X_L \\ &\vec U_1=(230\angle 0^\circ)+(10\angle -36,87^\circ)*(0,484\angle 0^\circ)+(10\angle -36,87^\circ)*(0,041\angle 90^\circ) \\ &\vec U_1=234,13 \ [V] \angle -0,63 ^\circ \\ &\Delta U=U_1-U_2=234,13-230=4,13 \[V] \end{align*}$

Derved er forskellen på de to beregningsmetoder meget lille, hvilket er grundet til, at den tilnærmet beregning ofte kan anvendes.

Spændingsfald 3-faset vekselsstrøm

Beregning af spændingsfald ved 3-faset belastninger deles op i to grupper – nemlig symmetrisk- og usymmetrisk belastninger. Beregning af usymmetrisk belastning er langt mere kompliceret end beregning på symmetriske belastninger. Jeg vil i det efterfølgende beregning af spændingsfald ved symmetriske og usymmetrisk belastninger.

Symmetrisk belastning

Ved beregning af spændingsfald på symmetrisk belastninger, skal vi tilbage til fremgangsmåden, der blev anvendt ved spændingsfaldsberegning af 1- og 2-faset belastninger. Beregner man på en symmetrisk belastning, vil der ske en ens spændingsfald i alle faserne. Symmetrisk belastning betyder, at der optages en samme størrelse strøm med samme faseforskydning i alle 3 faser.

Derfor ses der kun på en fase, når spændingsfald ved en symmetrisk 3-faset belastning beregnes. Derfor kan samme vektordiagram og teori anvendes til forklaring af spændingsfald ved symmetrisk belastninger.

Når vi beregner 3-faset spændingsfald, kan vi ligesom ved 1-faset spændingsfald beregne en tilnærmet resultat og et præcis resultat, hvor princippet er det samme.

Tilnærmet resultat

Hiver vi formlerne fra 1-faset tilnærmet spændingsfald frem igen har vi følgende formlern:

$\begin{align*} &\Delta U_f=I_B*R_l*cos\varphi_B \ (Resistiv belastning) \\ &\Delta U_f=I_B*(R_l*cos\varphi_B+X_l*sin\varphi_B) \ (Induktiv belastning) \\ &\Delta U_f=I_B*(R_l*cos\varphi_B-X_l*sin\varphi_B) \ (Kapacitib belastning) \end{align*}$

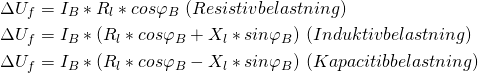
Bemærk, at jeg i formlerne har tilføjet f til $\Delta U$ , da vi beregner fasespændingsfaldet.

Derved skal den nye netspænding beregnes med forholdet mellem fase- og netspænding.

$U_{n2}=U_{n1}-\sqrt{3}*\Delta U_f$

Når vi snakker 3-faset spændingsfald, har vi ligeledes mulighed for at beregne den tilnærmet spændingsfald ud fra effekterne. Udledning af formlen, vil jeg ikke komme ind på. Dog er fordelen ved denne formel, at du beregne en netspændingsfald, og derved kan minimere beregninger.

$\Delta U_n=\frac{P*R_L+Q*X_L}{U_{n2}}$

Kendes spændingen ved brugsgenstanden ikke, kan $U_{n2}$ udskiftes med $U_{n1}$ uden det har videre betydning for resultatet.

Bemærk også, at du ikke kan tegne netspændingsfaldet ind på vektordiagrammet, og derfor er det et hjælpetal, der kommer af forholdet med fase- og netspænding.

Til sidst kan spænding U2 beregnes ud fra denne formel:

$U_{n2}=U_{n1}-\Delta U_n$

Usymmetrisk belastning

(Kommer snart)

Claus Hansen

Claus Hansen har med sin uddannelse som elektriker og maskinmester stor viden inden for elteorien og elinstallationer. Han ønsker med Elbogen.dk at vejlede og hjælpe studerende, private og folk i branchen med love, regler og teorien. Har du spørgsmål? Så send ham endelig en besked via kontaktformularen, der findes i de forskellige indlæg eller under kontakt i menuen.

Følge os på Facebook og bliv opdateret på de nyeste indlæg

Spørgsmål? Så send dem til mig

Kontakt mig her!