Jævnstrømsteori: Del 4 – Serie-, parallel- og blandedeforbindelser

Jævnstrøm også kaldet DC er grundlaget for el teori og eltekniske beregninger. Du er derfor nødsaget til at have styr på jævnstrømsteorien, før du går videre med mere komplicerede beregninger.

Med dette indlæg kan du finde el formler til beregning af serieforbindelser, parallelforbindelser og blandede forbindelser. Samtidig vil indlægget beskrive de enheder el beregning, og hvordan de beregnes. Hvis du ikke i forvejen kender til Ohms lov og effektberegning, vil jeg anbefale dig at læse mit indlæg omkring dette først.

Har du ris, ros eller blot ideer til hvad jeg kan ændre eller tilføje? Så skriv endelig via kontaktformularen i bunden af indlægget eller ved at vælge kontakt i toppen af menuen.

Jævnstrøm – Teorien

Der findes 2 typer strømme – nemlig jævnstrøm og vekselstrøm. For at markere, at vi taler jævnstrøm, kan symbolet med to streger anvendes (Figur 1). Jævnstrøm er en elektrisks strøm, hvor strømmen udelukkende føres i en retning. Vekselstrøm (AC) har derimod en varierende strøm, der variere fra et positiv værdi til et negativ værdi. I jævnstrøm siges det altid, at strømmen ledes fra plus til minus, hvilket dog ikke er teoretisk korrekt – dette er dog forklaret yderlig her her.

Der findes tre måder at koble sine jævnstrømskredsløb i:

Blandede forbindelser (Også kaldt kombinerede forbindelser) er en sammensætning af en eller flere serieforbindelser og parallelforbindelser. Blandede forbindelser skaber ofte problemer for mange, grundet vanskeligheder med adskillelse af forbindelserne. Jeg vil beskrive fremgangsmåden, så du får nemmere ved at løse opgaverne.

For at gøre beregningerne nemmer for dig selv, så er min anbefaling at følge disse 3 råd:

Tegn et kredsskema
Påfør værdierne på kredsskemaet
Lav eventuelt en tabel ved mere komplicerede beregninger

Det at tegne et kredsskema giver et visuelt overblik, og det er derved nemmere for dig, at skabe et overblik. Indsættes værdierne på kredsløbet øges overblikket yderligt. Er vi ude i mere komplicerede kredsløb – eksempelvis blandede forbindelser, kan en tabel være et brugbart værktøj for at sikre overblikket.

Serieforbindelser (Jævnstrøm DC)

Hvad er en serieforbindelse?

Figur 2: Vandsystem sammenlignet med en serieforbindelse

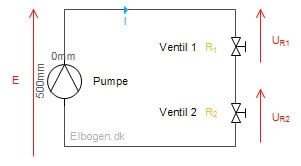
En af de mest simple forbindelser i el beregninger er serieforbindelserne i ved jævnstrøm. I en serieforbindelse er modstande koblet i forlængelse af hinanden. For at gøre forståelsen nem, sammenligner vi vores serieforbindelse med et rørsystem med pumpe og ventiler. Figur 2 viser et eksempel på et rørsystem. Vi forestiller os, at dette rørsystem skal cirkulere noget vand.

I vandkredsen er der to ventiler, som mindsker den indre diameter, og derved yder modstand mod vandstrømmen. Ventilerne kan derved sammenlignes med de resistive modstand i jævnstrømskredsløbet. De vil ofte have en fast værdi. Omdanner vi vores vandkreds til et elkredsløb, får vi vi kredsløbet på figur 3, hvor vi har 2 modstande og en jævnstrømsforsyning.

Kigger vi tilbage på vores rørsystem, og forestiller vi os, at vi har et vandflow gennem rørsystemet. Så kan vi konkludere, at den vandmængde der ledes igennem pumpen, også ledes igennem de to ventiler. Vandet kan ikke forsvinde fra systemet, med mindre der er en utæthed. Vandflowet kan vi sammenligne med strømmen i vores jævnstrøm kredsløb.

I en serieforbindelse er strømmen altid ens.

Hvordan ændrer vi så flowet i rørsystemet? Enten ændre vi på ventilerne eller trykket. På samme måde kan vi ændre strømmen i serieforbindelsen, hvis vi enten ændrer modstanden eller spændingen. Her kommer Ohms lov til sin ret:

$U=I*R$

Udfra ovenstående beskrivelse, kan vi matematisk opsætte ligningen for beregning af den samlede strøm ved jævnstrøm, hvis flowet er konstant:

$\sum I=I_1=I_2$

Spændinger i serieforbindelser

I serieforbindelse har vi en konstant strømmen igennem modstandene. For nu at definere spændingen i serieforbindelse, tager vi et kik på Kirchoffs anden lov (Også kaldt Kirchoffs spændingslov eller Kirchoffs maskeligning). Loven siger kort beskrevet, at den samlede elektromotoriske kraft i et kredsløb er lig med den samlede spændingsfald. Matematisk forklares det på følgende måde, hvis vi tager udgangspunkt i et kredsløb med en spændingsforsyning og 2 modstande.

$0=E-U_{R1}-U_{R2} \leftrightarrow E=U_{R1}+U_{R2}$

En spænding er et potentialeforskel der måles mellem to punkter. Placere du din spændingstesters to målepinde i samme position måler du 0 volt. Tager vi igen udgangspunkt i vores vandsystem, skal vores der være et trykforskel for at vandet kan cirkulere. I et kredsløb, skal der være et spændingsforskel, før der løber en strøm. I vandsystemet laver pumpen et trykforskel, der gør, at vandet cirkulerer rundt. I vores elkredsløb skaber vores spændingskilde (eksempelvis batteri eller spændingsforsyning) et spændingsforskel over dens udgangsklemmer (plus og minus). Spændingsforskellen over spændingskilden kaldes den elektromotoriske kraft (E). Elektromotorisk kraft anvendes både ved veksel- og jævnstrøm.

Hver gang vi indsætter en modstand i jævnstrømskredsløbet, vil der dannes et spændingsfald over denne. Den samlede spændingsfald er lig med den elektromotoriske kraft. Det betyder også, at har vi den samme elektromotoriske kraft, og indsættes endnu en modstand, vil spændingsfaldet over de øvrige modstande falde, da den nyindsatte modstand skal tage en del af den samlede spændingsfald. Ved indsættelse af endnu en modstand, vil den samlede modstand stige, og da vi har konstant spænding, vil strømmen fald.

Har du i dit jævnstrømskredsløb kun to modstande i serie, kan du beregne spændingsfaldet over hver modstand på en nemmere måde ved hjælp af spændingsdelingsformlen:

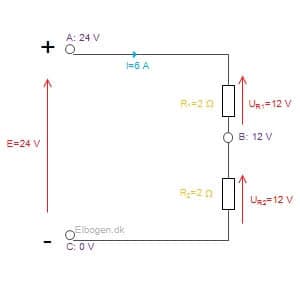
Figur 4: Serieforbindelse med spændingspile

$\begin{align*} &U_{R1}=E*\frac{R_1}{R_1+R_2} \\ &U_{R2}=E*\frac{R_2}{R_1+R_2} \end{align*}$

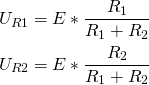
Eksempel på spændingsforskelle

Tages der udgangspunkt i figur 4, og måler vi spændingen forskellige steder i systemet, vil der kunne måles forskellige værdier. Anvendes et voltmeter (spændingstester), og måles der i mellem målepunkt C og A, vil vi måle den elektromotoriske kraft (i dette eksempel 24 volt), da du her måler forskellen over spændingskilden. Du vil samtidig også måle den samlede spændingsfald, da du også måler spændingsfaldet over både modstand R1 og R2. Måler du derimod imellem punkt C og B, måler du spændingsfaldet over modstand R2. Ved en elektromotorisk kraft på 24 volt og to ens modstande, ville denne være halvdelen af den elektromotoriske kraft. Derved vil du i eksemplet måle 12 volt. Måler du mellem punkt A og B, vil du måle spændingsfaldet over modstand R1. Da modstandene igen er ens, vil det igen være halvdelen af den elektromotoriske kraft – altså 12 volt.

Modstande og effekter i serieforbindelse

Den størsteberegningsforskel på serie- og parallelforbindelse er beregning af den samlede modstand eller erstatningsmodstanden. I serieforbindelse beregnes den samlede modstand ved at lægge de enkle modstande sammen. Dette kan beskrives matematisk på følgende måde:

$\sum R=R_1+R_2+...$

Har du den samlede modstand beregnet, og samtidig fået opgivet den påtrykte spænding, kan du beregne strømmen ud fra Ohms lov

$I=\frac{U}{R}$

Til sidst kan vi beregne effekterne i en serieforbindelse. Effektformlen blev beskrevet i den generelle teori, men genopfriskes lige her.

$P=U*I$

Ud fra effektloven kan de enkelte effekter hver modstand optager beregnes. Det gøres ud hver modstand data.

$P_1=U_{R1}*I_1=U_{R1}*I$

Har vi hver enkelt effekt opgivet, kan de ligeledes beregnes ved hjælp af almindelige sammenlægning.

$P=P_1+P_2+...$

Formler – Serieforbindelse DC

Før vi kigger på beregningseksempler til serieforbindelse ved jævnstrøm, kommer en opsummering af de forskellige udformning og sammensætninger af formler, jeg ligeledes beskrev i indlægget om generelt teori.

EffektSpændingStrømModstand

$\begin{align*} &P=U*I \\ &P=\frac{U^2}{R} \\ &P=I^2*R \\ &\sum P=P_1+P_2 \end{align*}$

$\begin{align*} &U=I*R \\ &U=\frac{P}{I} \\ &U=\sqrt{R*P} \\ &E=U_{R1}+U_{R2} \end{align*}$

$\begin{align*} &I=\frac{U}{R} \\ &I=\frac{P}{U} \\ &I=\sqrt{\frac{P}{R}} \\ &\sum I=I_1=I_2 \end{align*}$

$\begin{align*} &R=\frac{U}{I} \\ &R=\frac{P}{I^2} \\ &R=\frac{U^2}{P} \\ &\sum R=R_1+R_2 \end{align*}$

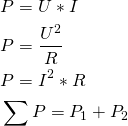
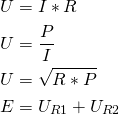
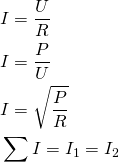
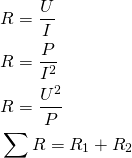
Derudover skal spændingsdelingsformlen huskes:

$\begin{align*} &U_{R1}=E*\frac{R_1}{R_1+R_2} \\ &U_{R2}=E*\frac{R_2}{R_1+R_2} \end{align*}$

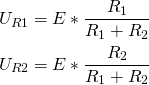
Beregningsekseksempler

Eksempel 1:Beregning af en simpel serieforbindelse

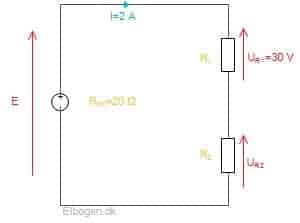
Der er i en kredsløb tilsluttet to modstande i serie, og den samlede modstand i kredsløbet er målt til 20 ohm. I kredsløbet er der en strømstyrke på 2 amperer . Spændingsfaldet over $R_1$ er målt til 30 volt. Kredsen forsynes med jævnstrøm. Beregn den elektromotoriske kraft (E), spændingsfaldet over $R_2$ ( $U_{R2}$ ), modstandene ( $R_1$ og $R_2$ ) og alle effekterne i kredsen ( $P_{tot}$ , $P_1$ og $P_2$ ).

Før vi begynder husker vi lige de to første af mine huskeregler:

Tegn et kredsskema
Indtast værdierne på kredsskemaet

Kredsskemaet er tegnet på figur 5, hvor værdierne er indsat.

Da vi har opgivet den samlede modstand og strømstyrke, kan vi beregne anlæggets elektromotoriske kraft (Den påtrykte spænding).

$E=I*\sum R=2*20=40 \ [V]$

Da vi ved, at den elektromotoriske kraft er lig med den samlede spændingsfald, kan vi beregne spændingsfaldet over modstand R2.

$U_{R2}=E-U_{R1}=40-30=10 \ [V]$

Derefter kan de to modstande beregnes

$\begin{align*} &R_1=\frac{U_{R1}}{I}=\frac{30}{2}=15 \ [\Omega] \\ &R_2=\frac{U_{R2}}{I}=\frac{10}{2}=5 \ [\Omega] \end{align*}$

Til sidst mangler vi kun at beregne effekterne i kredsen, hvilket vi gør via effektloven.

$\begin{align*} &\sum P=E*I=40*2=80 \ [W] \\ &P_1=U_{R1}*I=30*2=60 \ [W] \\ &P_2=P_{tot}-P_1=80-60=20 \ [W] \end{align*}$

Eksempel 2: Beregning af den elektromotoriske kraft

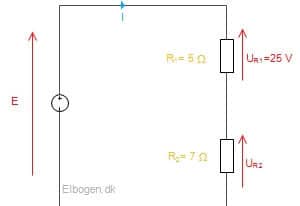
I et jævnstrømskredsløb er to forskellige modstande tilsluttet i serie. Modstandene har en værdi på 5 og 7 Ohm. Der er derudover målt et spændingsfald på 25V over modstand R1. Beregn kredsløbets elektromotoriske kraft.

Kredsløbet er skitseret på figur 6.

Der anvendes spændingsdelings formlen, hvor den elektromotoriske kraft isoleres (E):

$\begin{align*} &U_1=E*\frac{R_1}{R_1+R_2} \\ &\Updownarrow \\ &E=\frac{U_1*R_1+R_2}{R_1}=\frac{25*(5+7)}{5}=60 \ [V] \end{align*}$

[su_related_post_in_text][bibblio style=” bib–white-label bib–row-4 bib–title-only bib–portrait bib–square” query_string_params=e30=][/su_related_post_in_text]

Parallelforbindelse (Jævnstrøm DC)

Hvad er en parallelforbindelse?

Figur 7: Vandkreds sammenlignet med en paralllelforbindelse

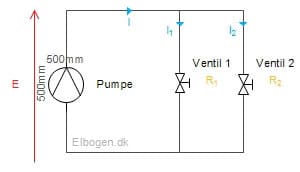
Beregning af parallelforbindelser er lidt anderledes i forhold til serieforbindelser. Sammenligner vi igen vores kredsløb med et rørsytem, hvor der denne gang er monteret to ventiler parallel over hinanden (figur 7).

Denne gang ledes vandet fra pumpen til første afgrening (mellem ventil 1 og 2). Her deler vandet sig, hvor mængden af vand til hver ventil afhænger af, hvor meget ventilerne er skruet i. Jo mere ventilen er skruet i, desto mere modstand ydes der, og derved vil mindre vand passere ventilen. Vandet samles igen efter at have passeret ventilerne. Derved er det den samme vandmængde der ledes fra pumpen, som der kommer til pumpen.

Sammenligner vi det med et el kredsløb (figur 8), hvor vandet er lig med strømmen, har vi en strøm der deler sig. Derfor kan vi beregne den samlede strøm ud fra strømmængden igennem de to ventiler.

$\sum I=I_1+I_2$

Denne formel kaldes også Kirchhoffs første lov (kaldes også Kirchhoffs knudepunktsligning eller Kirchoffs strømlov). Loven siger, at den strøm der kommer til en knudepunkt, er lig den strøm der forlader knudepunktet.

I en parallelforbindelse er spændingen altid ens. Det kan forklares ved, at du måler i samme punkt. Det vil sige, at uanset størrelserne på modstanden $R_1$ og $R_2$ , så vil spændingsfaldet være ens over begge modstande.

Ser vi på figur 8, og kigger på de forskellige punkter, kan vi se, at punkt 1 og 2 er ens, som har samme potentiale som pluspolen. Det samme er gældende med punkt 3 og 4, der har samme potentiale som minuspolen.

Derved kan vi matematisk forklar dette på følgende måde:

$E=U_{R1}=U_{R2}$

Har du i kredsløbet udelukkende to forskellige modstande, kan du beregne de forskellige strømme ved hjælp af strømdelingsformlen:

$\begin{align*} &I_{1}=\sum I*\frac{R_1*R_2}{R_1*(R_1+R_2)} \\ &I_{2}=\sum I*\frac{R_1*R_2}{R_2*(R_1+R_2)} \end{align*}$

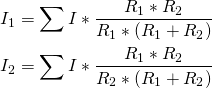
Modstand i parallelforbindelse

Der hvor parallelforbindelse især skiller sig ud i forhold til serieforbindelse er ved beregning af modstand. Når en parallelforbindelses samlede modstand beregnes, vil den altid blive mindre end den mindste enkle modstand. Dette skyldtes, at i en parallelforbindelse etableres hver modstand nye strømveje. Hvis vi ser det på pumpesystemet, vil hver ny ventil i parallel give mulighed for gennemløb af mere vand ved samme tryk. Derved har vi mindsket modstanden. Ved anvendelse af Ohms lov, kan vi bevise at når modstanden mindskes og spændingen holdes konstant, vil den samlede strøm øges.

For at beregne den samlede modstand i parallelforbindelse, anvendes følgende formel:

$\begin{align*} &\frac{1}{\sum R}=\frac{1}{R_1}+\frac{1}{R_2} \\ &\Updownarrow \\ &\sum R=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}}=(\frac{1}{R_1}+\frac{1}{R_2})^{-1} \end{align*}$

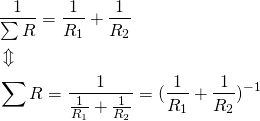
Har du kun har modstande i samme størrelse, kan du beregne den samlede modstand nemmere ved at dele modstandstørrelse med antallet af modstande:

$\sum R=\frac{R}{antallet}$

Effekt i parallelforbindelser

Beregning af effekt i parallelforbindelse er fuldstændig ens med beregningerne i serieforbindelser. Du skal blot huske, at i paralleforbindelse er spænding ens imens strømmen varierer fra modstand til modstand. Effektloven anvendes derved igen

$\begin{align*} &P=I*U \\ &P_1=U*I_1 \\ &P_2=U*I_2 \end{align*}$

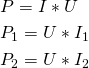
Formler- Parallelforbindelser DC

Her findes de nødvendige formler til beregning af parallelforbindelser

EffektSpændingStrømModstand

$\begin{align*} &P=U*I \\ &P=\frac{U^2}{R} \\ &P=I^2*R \\ &\sum P=P_1+P_2 \end{align*}$

$\begin{align*} &U=I*R \\ &U=\frac{P}{I} \\ &U=\sqrt{R*P} \\ &E=U_{R1}=U_{R2} \end{align*}$

$\begin{align*} &I=\frac{U}{R} \\ &I=\frac{P}{U} \\ &I=\sqrt{\frac{P}{R}} \\ &\sum I=I_1+I_2 \end{align*}$

$\begin{align*} &R=\frac{U}{I} \\ &R=\frac{P}{I^2} \\ &R=\frac{U^2}{P} \\ &\sum R=(\frac{1}{R_1}+\frac{1}{R_2})^{-1} \end{align*}$

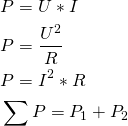
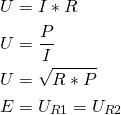
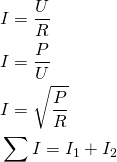
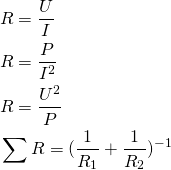
Derudover skal strømdelingsformlen huskes:

$\begin{align*} &I_{1}=\sum I*\frac{R_1*R_2}{R_1*(R_1+R_2)} \\ &I_{2}=\sum I*\frac{R_1*R_2}{R_2*(R_1+R_2)} \end{align*}$

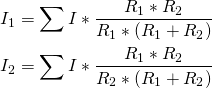
Beregningsekseksempler

Eksempel 1: Beregning af den samlede modstand

Parallelforbindelse eksempel 1 — Figur 9: parallelforbindelse eksempel 1

I et kredsløb er der parallelforbundet 3 modstande på henholdsvis 3, 5 og 7 Ohm. Hvor stor er den samlede modstand?

Modstanden beregnes ud fra den reciprokke værdi:

$\begin{align*} &\sum R=(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3})^{-1} \\ &\Updownarrow \\ &R_{tot}=(\frac{1}{3}+\frac{1}{5}+\frac{1}{7})^{-1}=1,5 \ [\Omega] \end{align*}$

Figur 10: Parallelforbindelse eksempel 2

Eksempel 2: Beregning af strømmen

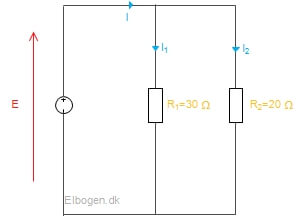
I et kredsløb er der parallelkoblet 2 modstande på henholdsvis 30 ohm og 20 ohm. Den samlede strøm er 1 Ampere.

Beregn strømmen gennem henholdsvis modstand R1 og R2’s:

Strømdelingsformlen anvendes til beregning af den ene strøm igennem modstand R1:

$\begin{align*} &I_1=\sum I*\frac{R_1*R_2}{R_1*(R_1+R_2)} \\ &\Updownarrow \\ &I_1=1*\frac{30*20}{30*(30+20)}=0,4 \ [A] \end{align*}$

Derefter kan strømmen igennem modstand R2 findes ved Kirchoff første lov:

$I_2=I-I_1=1-0,4=0,6 \ [A]$

Eksempel 3: Beregning af en simpel parallelforbindelse

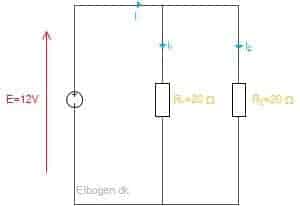
Figur 11: Parallelforbindelse eksempel 3

I et kredsløb er der tilsluttet to modstande på 20 ohm. Kredsløbet elektromotoriske kraft er 12V. Beregn kredsen strømme, kredsen samlede modstand, den samlede effekt og modstand R1 og R2’s optaget effekt.

$\sum R{tot=\frac{R_{1,2}}{antal}=\frac{20}{2}=10 \ [\Omega]$

Herefter kan den samlede strøm beregnes:

$\sum I=\frac{U}{\sum R}=\frac{12}{10}=1,2 \ [A]$

Da der er to lige store modstande, vil de gennemløbes af den samme strømstyrke. Derfor kan strømmen igennem R1 og R2 findes således:

$I_1=I_2=\frac{\sum I}{2}={1,2}{2}=0,6 \ [A]$

Herefter mangler vi blot at beregne elkredsløbets effekter. Effekten af de to modstande er ens, da de har samme størrelse:

$\begin{align*} &P_1=P_2=E*I_1=12*0,6=7,2 \ [W] \\ &\sum P=P_1+P_2=7,2+7,2=14,4 \ [W] \end{align*}$

[su_related_post_in_text][bibblio style=” bib–white-label bib–row-4 bib–title-only bib–portrait bib–square” query_string_params=e30=][/su_related_post_in_text]

Blandede forbindelse (Jævnstrøm DC)

Nu har vi været igennem både serie- 0g parallelforbindelse. Derved har vi været igennem alt teori til blandede forbindelser – nemt ikke? Ofte er svaret dog nej. Det skyldtes, at blandede forbindelse kan være vanskelig at dele op i serie- og parallelforbindelser. Blandede forbindelser (eller kombinerede forbindelser, som det også kaldes) er en blanding af både serie- og parallelforbindelser. Det er derfor vigtig, at man får erfaring i at skille dem ad.

Ved serieforbindelser har vi følgende regler:

Strømmen er ens gennem hele kredsløbet
Spændingsfaldet deler sig ud over de enkelte modstande
Modstanden lægges sammen almindeligvis

Ved parallelforbindelser har vi følgende regler:

Strømmen deler sig ud i hver afgrening
Spændingsfaldet er er ens over alle komponenter
Modstanden lægges sammen med den reciprokke værdi.

Jeg har derudover to huskeregler, der kan hjælpe dig på vej:

Hvis to eller flere modstande gennemløbes af samme strøm, kan de lægges sammen efter reglerne for serieforbindelse.

Hvis to eller flere modstande har samme spændingspotentiale over sig, kan de lægges sammen efter reglerne for parallelforbindelse

Teknikken bag blandede forbindelser ved jævnstrøm er, at du skal mindske antallet af modstande ved at lægge dem sammen. Derved beregne du en erstatningsmodstand, og dervedl simplificere kredsløbet.

Modstande i blandede forbindelser

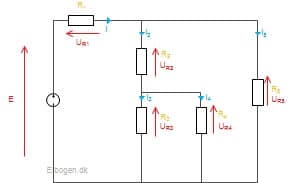
Figur 12 symboliserer en blandet forbindelse med fem modstande. Vores mission er, at mindske kredsløbet og beregne den samlede modstand. Først dannes et overblik over, om en eller flere modstande gennemløbes af samme strøm. Det har vi ikke. Derfor kigges der efter om nogle modstande har samme spændingspotentiale over sig, hvilket modstand $R_3$ og $R_4$ har.

$U_{R3}=U_{R4}$

Derfor beregnes en erstatningsmodstanden for $R_3$ og $R_4$ efter reglerne for parallelforbindelse.

$R_{34}=(\frac{1}{R_3}+\frac{1}{R_4})^{-1}$

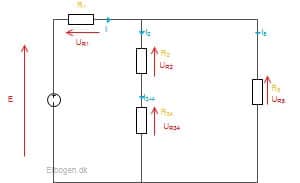
Herefter tegnes en nye kredsskema, hvor erstatningsmodstanden udskiftes med $R_3$ og $R_4$ . Dette er gjort på figur 13.

Der kigges nu igen efter, om flere modstande gennemløbes af samme strøm. I dette tilfælde gennemløbes modstanden $R_2$ og erstatningsmodstanden $R_{34}$ af den samme strøm.

$I_2=I_{34}=I_3+I_4$

Derved beregnes erstatningsmodstand for disse to modstande efter reglerne for serieforbindelse:

$R_{234}=R_2+R_{34}$

Dette reducere den blandede forbindelse til figur 14. Derved er kredsløbet langt mere overskuelig.

Kredsløbet er stadigvæk en blandet forbindelse, og derfor kigger vi igen, om flere modstande gennemløbes af den samme strøm. Da det ikke er tilfældet, kigger vi efter om der er modstande med samme spændingspotentiale. Det har erstatningsmodstanden $R_{234}$ og modstanden $R_5$ . Derfor lægges disse to modstande sammen efter reglerne for parallelforbindelse.

$R_{2345}=(\frac{1}{R_{234}}+\frac{1}{R_5})^{-1}$

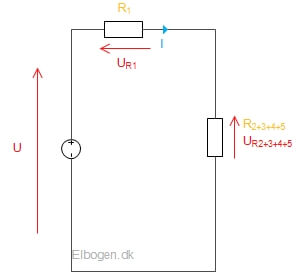
Erstatningsmodstanden tegnes ind på en ny kredsskema (figur 15), og derved er vores blandede forbindelse omdannet til en serieforbindelse, hvilket gør det nemmere at beregne den samlede modstand i kredsen.

Derfor lægges erstatningsmodstanden $R_{2345}$ sammen med modstand $R_1$ , hvorefter den samlede modstand bliver beregnet:

$\sum R=R_1+R_{2345}$

Herefter kanden samlede strøm beregnes, hvorefter du går baglæns, og beregner de forskellige spændingsfald, samt strømme igennem de forskellige modstande. Jeg vil i beregningseksemplet her under beregne alle spændingerne, strømme, modstande og effekter. Herefter er det blot at øve sig på forskellige opgaver.

Beregningseksempel

Eksempel 1: Beregning af en blandet forbindelse

Figur 16: Blandede forbindelser eksempel 1

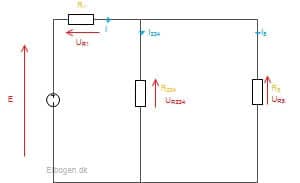
Der er i en blandet forbindelse indsat 5 modstande. Figur 16 indeholder opbygning og værdierne, der forsynes med jævnstrøm.

Eksemplet er det samme, som vi anvendte i overstående gennemgang, hvor vi dog her beregner kredsløbet med værdier.

Går vi tilbage til starten af dette indlæg havde jeg tre anbefalinger

Tegn et kredsskema
Påfør værdierne
Lav en tabel

Derved laves en tabel, hvor værdierne kan indtastes. Værdier skrevet med fed, er værdier der er opgivet på forhånd. De øvrige værdier finder igennem eksemplet.

	Samlet	R1	R2	R3	R4	R5
Modstand	12 Ω	2 Ω	10 Ω	15 Ω	12 Ω	25 Ω
Strøm	2 A	2 A	1,2 A	0,533 A	0,667 A	0,8 A
Spænding	24 V	4 V	12 V	8 V	8 V	20 V
Effekt	48 W	8 W	14,4 W	4,26 W	5,34 W	16 W

Skab et overblik

Først skabes et overblik. Hvilke værdier kan beregnes, og hvilke er ens. Tager vi et kig på modstand R1 er denne i serie med resten af kredsen. Dermed må strømmen igennem $R_1$ være lig den samlede strøm.

$I_1=\sum I$

Forsætter vi med at kigge på modstand R1, kender vi både strøm og modstand. Dette betyder, at ved hjælp af Ohms lov, kan vi beregne spændingsfaldet over modstanden.

$U_{R1}=I_1*R_1=2*2=4 \ [V]$

Vi kan samtidig beregne modstandens optaget effekt. Vi kan gøre dette på flere måder.

$\begin{align*} &P_1=U_{R1}*I_1=4*2=8\ [W] \\ &P_1=\frac{U_{R1}^2}{R_1 }=\frac{4^2}{2}=8 \ [W] \\ &P_1=I_1^2*R_1=2^2*2=8 \ [W] \end{align*}$

Derved har vi beregnet samtlige værdier for modstanden R1. I næste step skal vi undersøge, hvad vi kan beregne. Kigger vi i tabellen, kan vi se, vi kender to værdier omkring den samlede belastning. Det er den elektromotoriske kraft og strømmen. Derved kan vi beregne modstanden og effekten.

$\begin{align*} &\sum R=\frac{E}{\sum I}=\frac{24}{2}=12 \ [\Omega] \\ &P=E*\sum I=24*2=48 \ [W] \end{align*}$

Beregning af spændingsfald

Da vi har modstand R1 i serie med parallelforbindelsen af R2-R4 og R5, kan vi anvende regler for serieforbindelse til beregning af spænding. Her er spændingsfaldet lig med den elektromotoriske kraft. Derfor må de følgende udsagn være sandt:

$\begin{align*} &E=U_{R1}+U_{R2}+U_{R3} \Leftrightarrow 24=4+U_{R2}+U_{R3} \\ &E=U_{R1}+U_{R2}+U_{R4} \Leftrightarrow 24=4+U_{R2}+8 \\ &E=U_{R1}+U_{R5}\Leftrightarrow 24=4+U_{R5} \end{align*}$

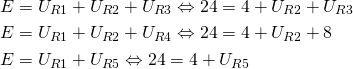
Der er flere af ligningerne, der kun har en ubekendt. Derved kan de let beregnes. Den første ligning har to ubekendte, men kigger vi på modstand R3, kan det ses at denne er parallelt med R4. Derved kan vi ved hjælp af reglerne for parallelforbindelse konstaterer, at de to modstande har samme spændingspotentiale over sig. Derved er følgende udsagn korrekt:

$U_{R3}=U_{R4}=8 [V]$

Da ligning 1 og 2 er inderholder ens værdier, beregnes den første kun i følgende ligninger:

$\begin{align*} &E=U_{R1}+U_{R2}+U_{R3} \Leftrightarrow U_{R2}=E-U_{R1}-U_{R3}=24-4-8=12 V \ [V] \\ &E=U_{R1}+U_{R5}\Leftrightarrow U_{R5}=E-U_{R5}=24-4=20 \ [V] \end{align*}$

Beregning af de øvrige værdier

Kigger vi på modstand R2, har vi nu to forskellige værdier, hvilket giver os mulighed for at beregne resten. Derved kan vi beregne strømmen og effekten for modstand R2.

$\begin{align*} &I_2=\frac{U_{R2}}{R_2}=\frac{12}{10}=1,2 \[A] \\ &P_2=U_{R2}*I_2=12*1,2=14,4 \ [W] \end{align*}$

Nu kender vi strømmen til og fra den ene afgrening efter modstand R1. Derfor kan vi beregne strømmen gennem modstand R5.

$I_5=\sum I-I_2=2-1,2=0,8 \ [A]$

Herefter kender vi både strøm og spænding, og derved kan modstand og effekt beregnes:

$\begin{align*} &R_5=\frac{U_{R5}}{I_5}=\frac{20}{0,8}=25 \ [\Omega] \\ &P_5=U_{R5}*I_5=20*0,8=16 \ [W] \end{align*}$

Herefter mangler vi kun at beregne de sidste to modstand R3 og R4. Vi kender R3’s modstand og spænding, og derved kan strøm og effekt beregnes:

$\begin{align*} &I_3=\frac{U_{R3}}{R_3}=\frac{8}{15}=0,533 \ [A] \\ &P_3=U_{R3}*I_3=8*0,533=4,26 \ [W] \end{align*}$

De sidste værdier vi skal beregne er modstand R4’s værdier. Da vi ved fra parallelforbindelser, at strømmen deler sig, ved vi ledes, at strømmen igennem R2 deles mellem R3 og R4. Derved kan vi beregne strømmen igennem R4:

$I_4=I_2-I_3=1,2-0,533=0,667 \ [A]$

Derved kan de resterende værdier beregnes:

$\begin{align*} &R_4=\frac{U_{R4}}{I_4}=\frac{8}{0,667}=12 \ [\Omega] \\ &P_4=U_{R4}*I_4=8*0,667=5,336 \ [W] \end{align*}$

Derved er alle værdier beregnet, og eksemplet er løst.

Spørgsmål?

Har denne artikel hjulpet dig med at forstå jævnstrøm, eller har du ris, ros eller blot ideer til forbedring? Så kontakt mig endelig, og hver med til at forbedre siden. Anvend kontaktformularen herunder, hvor du også er velkommen til at sende spørgsmål angående jævnstrøm og dens teori til mig.

Claus Hansen

Claus Hansen har med sin uddannelse som elektriker og maskinmester stor viden inden for elteorien og elinstallationer. Han ønsker med Elbogen.dk at vejlede og hjælpe studerende, private og folk i branchen med love, regler og teorien. Har du spørgsmål? Så send ham endelig en besked via kontaktformularen, der findes i de forskellige indlæg eller under kontakt i menuen.

Følge os på Facebook og bliv opdateret på de nyeste indlæg

Spørgsmål? Så send dem til mig

Kontakt mig her!