Der findes forskellige former for elektriske love, der anvendes til beregning af elteori. Er du bare lidt bekendt inden for el, kender du sikkert allerede Ohms lov og effektformlen. I dette indlæg vil jeg løbende tilføje de elektriske love, der anvendes til beregning af elkredsløb.
Rigtig mange af lovene kender du sikkert i forvejen – eller i hvert fald teorien bag dem.
Ohms lov
Ohms lov beskriver sammenhængen mellem elektrisk spænding (U), strømstyrke (I) og modstand (R) i en elektrisk kreds. Loven siger, at spændingen over en modstand er lig med strømmen gennem modstanden ganget med modstanden. Matematisk udtrykkes det som:
![]()
Dette gør det muligt at beregne en af variablerne, hvis de to andre er kendt. Ohms lov er en grundlæggende regel inden for elteori og bruges bredt til beregning af elektriske kredsløb.
Eksempler på Ohms lov
I en given kredsløb, er der en påtrykt spænding på 10V, og der er en modstand på 5 Ohm. Beregn strømmen i kredsløbet.
![Rendered by QuickLaTeX.com \begin{align*} &U=I*R \\ &\Updownarrow \\ &I=\frac{U}{R} \\ &\Updownarrow \\ &I=\frac{10}{5} =2\ [A] \end{align*}](https://elbogen.dk/wp-content/ql-cache/quicklatex.com-3c3bb417ef5f9d0da26af795879a7144_l3.png)
Strømmen i kredsløbet er derfor 2 ampere.
Effektloven
Effektloven er en grundlæggende formel inden for elektriske kredsløb, som beskriver forholdet mellem elektrisk effekt (P), spænding (U), og strøm (I).
Formlen lyder:
![]()
Hvor:
- P står for effekt målt i watt (W).
- U står for spænding målt i volt (V).
- I står for strømstyrke målt i ampere (A).
Formlen siger, at den elektriske effekt, der udvikles i et kredsløb, er produktet af spændingen og strømstyrken. Med andre ord angiver effektloven, hvor meget energi der omsættes pr. sekund i et elektrisk kredsløb.
Eksempel på beregning med effektloven
Lad os sige, at vi har en pære, der får en spænding på 24 volt, og strømmen, der løber igennem den, er 0,5 ampere. Vi ønsker at finde ud af, hvor meget effekt (P) pæren bruger.
Vi anvender formlen:
![]()
Hvor:
- U=24 [V]
- I=0,5 [A]
Beregningen bliver:
![]()
Pæren bruger altså 12 watt. Dette betyder, at pæren omsætter 12 joule energi pr. sekund, når den er tændt.
Kirchhoffs love
Nogle af de mest kendte love er Kirchhoffs love. De er generelt anvendt som Kirchhoffs 1. og 2. lov eller som Kirchhoffs strømlov og spændingslov.
Kirchhoffs 1. lov – Strømloven
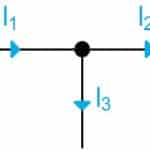
Kirchhoffs første lov kaldes også Strømloven eller knudepunktsligningen. Loven siger, at den strøm, der kommer til et knudepunkt er lig med den strøm der forlader et knudepunkt. Denne regel er baggrunden for beregning af parallelforbindelser ved både jævnstrøm og vekselstrøm.
Tager vi et kig på figur 1, har vi et knudepunkt, hvor strømmen kommer til og deles. Vi har en samlet strøm der kommer ind (![]() ). Strømmen deles herefter ud i strømmene i den lodrette og vandrette linje (
). Strømmen deles herefter ud i strømmene i den lodrette og vandrette linje (![]() &
& ![]() ). For at opfylde Kirchhoffs første lov, må ligning for dette scenarie være:
). For at opfylde Kirchhoffs første lov, må ligning for dette scenarie være:
![]()
Eksempler på Kirchhoffs 1. lov
Eksemplerne findes også i videoen
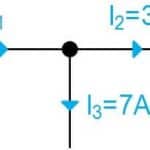
Eksempel 1
Figur 2 illustrerer eksempel 1 , hvor strømmen ledes til knudepunktet gennem ![]() , hvorefter det ledes væk igennem
, hvorefter det ledes væk igennem ![]() og
og ![]() . Derved kan formlen for strømmen der ledes til knudepunktet hurtig opsættes.
. Derved kan formlen for strømmen der ledes til knudepunktet hurtig opsættes.
![Rendered by QuickLaTeX.com \begin{align*} &I_1=I_2+I_3 \\ &\Updownarrow \\ &I_1=3+7=10 \ [A] \end{align*}](https://elbogen.dk/wp-content/ql-cache/quicklatex.com-4fcb39eefd7fee2ece8b8fa687de3107_l3.png)
Der vil derfor ledes en strøm på 10 ampere til knudepunktet.

Eksempel 2
Figur 3 illustrerer endnu et eksempel. Her har vi to strømme til knudepunktet (![]() &
& ![]() ), samt en strøm der løber fra knudepunktet (
), samt en strøm der løber fra knudepunktet (![]() ). Strømmen i
). Strømmen i ![]() er 7 ampere og er lig med strømmen der løber til knudepunktet.
er 7 ampere og er lig med strømmen der løber til knudepunktet. ![]() er 3 ampere.
er 3 ampere. ![]() skal findes.
skal findes.
![Rendered by QuickLaTeX.com \begin{align*} &I_3=I_1+I_2 \\ &\Updownarrow \\ &I_1=I_3-I_2 \\ &\Updownarrow \\ &I_1=7-3=4 \ [A] \end{align*}](https://elbogen.dk/wp-content/ql-cache/quicklatex.com-24f52f37b1eb83aaa51951f0370c1e63_l3.png)
Kirchhoffs 2. lov – Spændingsloven
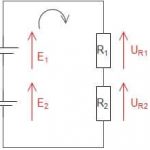
Kirchhoffs 2. lov kaldes og spændingsloven eller maskeligningen. Den siger at summen af spændingsforskelene regnet med fortegn er lig med nul. Oversat til noget andet forstålig betyder det, at summen af den spænding der påtrykkes et kredsløb er lig med den samlede spændingsfald i kredsløbet. Denne reglen anvendes generelt i serieforbindelse beregning ved jævnstrøm og vekselstrøm.
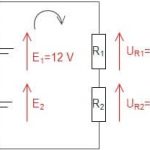
Tages der et kig på figur 4, kan det forklares, at den spænding som spændingskilde 1 og 2 levere er lig med det spændingsfald over modstand R1 og R2.
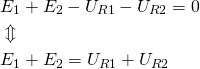
Eksempler på Kirchhoffs 2. lov
Eksemplerne er også vist i videoen
Eksempel 1
Figur 5 viser et eksempel på Kirchhoffs 2. lov. Vi har to spændingskilder, hvor den ene er ubekendt. Derudover har vi to modstande med en spændingsfald på henholdsvis 10 og 17 Volt.
Vi kender fra teorien følgende:
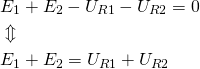
For at beregne ![]() , skal denne isoleres. Dette gøres ved at flytte spændingskilde
, skal denne isoleres. Dette gøres ved at flytte spændingskilde ![]() over på modsatte side af lighedstegnet.
over på modsatte side af lighedstegnet.
![Rendered by QuickLaTeX.com \begin{align*} &E_2=-E_1+U_{R1}+U_{R2} \\ &\Updownarrow \\ &E_2=-12+10+17=15 \ [V] \end{align*}](https://elbogen.dk/wp-content/ql-cache/quicklatex.com-fc06701bf6c3530c6ddd73da8a4758c1_l3.png)


