Dimensionering af boliginstallationer eksempel

Hjem
>>
Dimensionering
>>
Dimensionering af boliginstallationer eksempel

Dette indlæg omhandler dimensionering af boliginstallationer efter den nye standard DS/HD 60364. Da SB6 blev anvendt, indeholdte den forenklede danske regler, der gjorde boligdimensionering nemmere. Her skulle du slå op i en tabel for at sikre, at installationen var dimensioneret korrekt. I dag er opgaven lidt mere kompliceret, og du skal udføre flere beregninger. Samtidig er 75% reglen udgået. Jeg vil i dette eksempel dimensionere i henhold til DS/HD60364.

Denne gennemgang af bolig tager udgangspunkt i teorien anvendt i dette indlæg.

Ved dimensionering af en installation, er der en vigtig og gylden formel.

$I_z\geq I_n\geq I_B$

Det betyder, at kablets strømværdi skal være større eller lig med beskyttelsesudstyrets strømværdi, og at beskyttelsesudstyrets strømværdi skal være større eller lig med belastningen.

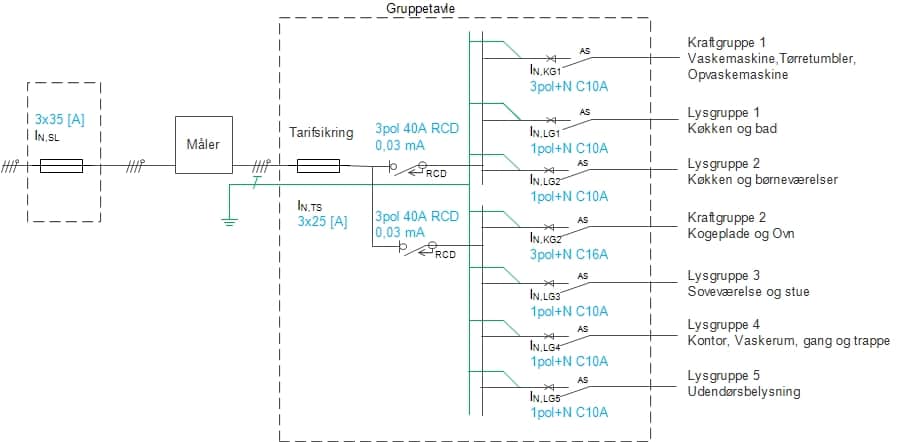
Installationsoverblik

Jeg tager udgangspunkt i en fiktiv husinstallation.

Huset størrelse: 153 m2.

Kraftforbruger:

Vaskemaskine og tørretumbler i vaskerummet
- Vaskemaskine 2300 Watt L+N 230V (5 meter fra tavlen)
- Tørretumbler 800 Watt L+N 230V (5 meter fra tavlen)
Ovn og kogeplade i køkkenet
- Kogeplade 2 faser minimum 16A (20 meter fra tavlen)
- Ovn 3400 Watt L+N 230V (18 meter fra tavlen)
Opvaskemaskine i køkkenet
- Opvaskemaskine 1900 Watt L+N 230V (22 meter fra tavlen)

Lysgrupper:

Efter Installationsbekendtgørelsen paragraf 56, skal der minimum være en lysgruppe pr. påbegyndt 50 m2.

Derved skal der være minimum 4 grupper, da huset er 153 m2.

Lysgruppe 1: Køkken og bad: Afstand til fjerneste del af installation er 28 meter.
Lysgruppe 2: Køkken og børneværelser: Afstand til fjerneste del af installationen er 32 meter.
Lysgruppe 3: Soveværelse og stue: Afstand til fjerneste del af installationen er 12 meter.
Lysgruppe 4: Kontor, vaskerum, gang og trappe: Afstand til fjerneste del af installationen er 23 meter
En ekstra gruppe til udendørsbelysning med den længste afstand på 52 meter

Det arbejdes på et TT jordingssystem.

Dimensionering af eltavlen

En tavlen er installationens knudepunkt, og skal derved klare den samlede belastning af installationen. For at beregne forbruget af en hel installation, skal vi have delt de forskellige grupper ud på faserne. Derved beregnes de enkelte forbrugers belastning. Det antages at alle brugsgenstande har en effektfaktor på 1, og der derfor ingen induktiv belastning er.

Valg af kraftgrupper og lysgrupper

Kravene til valg af automatsikring

For at vælge en automatsikring er der krav, der skal overholdes.

$I_n \geq I_B$

$U_e \geq U_n$

$I_{cu/cs} \geq I_{kmax}$

$I_{n,kb,max} \leq I_{k,min}$

[su_read_also pic1=”https://elbogen.dk/wp-content/uploads/2019/04/Automatsikring.jpg” link1=”https://elbogen.dk/dimensionering-teori/#Valg_af_automatsikring”]Hvordan vælges en automatsikring? [/su_read_also]

Kraftgruppe 1:

Jeg har valgt at køre et kabel fra kraftgruppen til vaskemaskine og tørretumbler og et andet kabel fra kraftgruppen til opvaskemaskinen. De fordeles de på hver deres fase. Opvaskemaskine monteres på L1, tørretumbler på L2 og vaskemaskinepå L3.

Opvaskemaskine: $I_{OM}=\frac{P}{U*cos\phi}=\frac{1900}{230*1}=8,26 [A]$

Tørretumbler: $I_{TT}=\frac{P}{U*cos\phi}=\frac{800}{230*1}=3,48 [A]$

Vaskemaskine: $I_{VM}=\frac{P}{U*cos\phi}=\frac{2300}{230*1}=10 [A]$

Valg: 3pol+N C10 A Siemens 5SY6 automatiksikring med følgende data:

$I_n=10 [A]$
$U_e=400 [V]$
$I_{cs}=6 [kA]$
$I_{n,kb,max}=10*I_n=10*10=100 [A]$

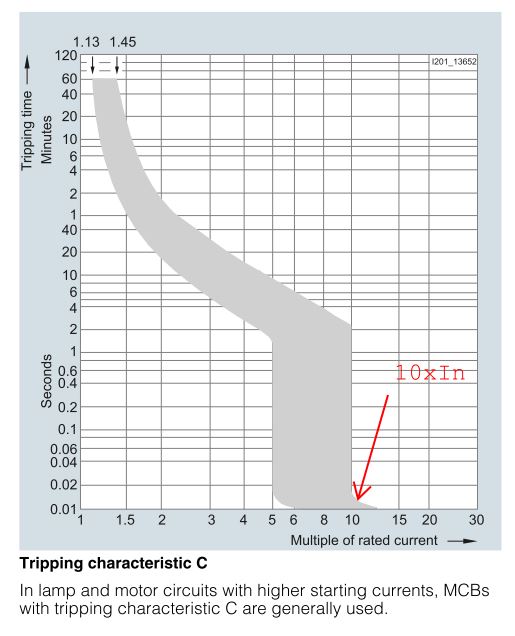
Dimensionering automatsikring — Billede fra Siemens

Kontrol:

$10 [A]\geq 10 [A] \rightarrow OK$
$400 [V] \geq 400 [V] \rightarrow OK$
$6 [kA] \geq I_{kmax} \rightarrow$ Tjekkes senere
$100 [A] \leq I_{k,min} \rightarrow$ Tjekkes senere

Kraftgruppe 2:

Ovn monteres på L1 og kogepladen monteres på L2 og L3

Kogeplade: $I_{KP}=16 [A]$

Ovn: $I_{OVN}=\frac{P}{U*cos\phi}=\frac{3400}{230*1}=14,78 [A]$

Valg: 3pol+N C16 A Siemens 5SY6 automatiksikring med følgende data:

$I_n=16 [A]$
$U_e=400 [V]$
$I_{cs}=6 [kA]$
$I_{n,kb,max}=10*I_n=10*16=160 [A]$

Kontrol:

$16 [A]\geq 16 [A] \rightarrow OK$
$400 [V] \geq 400 [V] \rightarrow OK$
$6 [kA] \geq I_{kmax} \rightarrow$ Tjekkes senere
$160 [A] \leq I_{k,min} \rightarrow$ Tjekkes senere

Lysgrupper:

Lysgrupper vælges til 10 A. I bolig anvendes der ofte 10 eller 13 A. Jeg har valgt at anvende 10 A, da du ofte kan nøjes med 1,5 kvadrat kabel.

Valg: 5 stk. 1pol+N C10 A Siemens 5SY6 automatiksikring med følgende data:

$I_n=10 [A]$
$U_e=400 [V]$
$I_{cs}=6 [kA]$
$I_{n,kb,max}=10*I_n=10*10=100 [A]$

Kontrol:

$10 [A]\geq 10 [A] \rightarrow OK$
$400 [V] \geq 400 [V] \rightarrow OK$
$6 [kA] \geq I_{kmax} \rightarrow$ Tjekkes senere
$100 [A] \leq I_{k,min} \rightarrow$ Tjekkes senere

Fordeling af grupperne og beregning af belastningen

L1: Lysgruppe 1 og 4 og kraftgruppe 1 og 2
L2: Lysgruppe 2 og 5 og kraftgruppe 1 og 2
L3: Lysgruppe 3 og kraftgruppe 1 og 2

Derved kan den maksimale belastning på faserne beregnes:

$I_{L1,maks}=I_{LG1}+I_{LG4}+I_{OM}+I_{OVN}=10+10+8,26+14,78=43,04 [A]$

$I_{L2,maks}=I_{LG2}+I_{LG5}+I_{TT}+I_{KP}=10+10+3,48+16=39,48 [A]$

$I_{L3,maks}=I_{LG3}+I_{VM}+I_{KP}=10+10+16=36 [A]$

Da det er en boliginstallation, forventes det ikke, at denne belastning nogensinde opnås. Derfor regnes der generelt med en samtidigfaktor (SF), der er med til at reducere forbruget. Udover det, skal der også tages højde for yderlig udvidelse af tavlen – en såkaldt udvidelsesfaktor (UF). Vi arbejder med en SF på 45% og en udvidelse 20%.

$SF=0,45$

$UF=1,2$

Derved kan strømmen til dimensionering beregnes, hvor den mest belastede fase anvendes – i dette tilfælde L1 med en maksimal belastning på 43,04 A.

$I_B=43,04*0,45*1,2=23,24 [A]$

Valg af fejlstrømsafbryder

Da der i henhold til den nye standard, skal være 2 RCD’er i ens installation, vælger jeg i dette tilfælde at anvende 2 stk. 3pol+N 40A RCD med en udløserstrøm på 30 mA (HPFI). Da jeg har en maksimalt belastning på hele installationen på 23,24 A, er 40 A rigeligt. I princippet kunne en mindre model anvendes, men da 40A oftest er billigst, vælges denne.

Valg: 2 stk. 3pol+N 40A HPFI afbryder (RCD med en mærkeudløserstrøm på 30 mA)

Kontrol: $40 [A]\geq 23,24 [A] \rightarrow OK$

Valg af tarifsikringer

Derefter vælges en sikring til tarifsikring, der kan klare overstående belastningsstrøm. Hvorfor vælger jeg at anvende tarifsikringer? Det er steder i landet, hvor det er et krav. Er der ikke krav til tarifsikringer, kan denne undlades, og sikringerne i kabelskabet kan anvendes til både OB og KB af stikledningen.

Valg: 3 stk. 25 A D02 sikringer

Kontrol: $25 [A]\geq 23,24 [A] \rightarrow OK$

Valg af sikring i kabelskab

For at kunne vælge sikringer i kabelskabet, skal det sikres, at disse har en sådan størrelse, at selektivitet opnås mellem dem og tarifsikringerne. Dette kan gøres på flere måder. Du kan blandt andet sammenligner kablerens smeltekurver eller vælger at gange med faktor 1,6. 1,6 kommer fra DS/HD 60364 afsnit 536.4.1.2.3.

[su_read_also pic1=”https://elbogen.dk/wp-content/uploads/2019/04/Bestemmelse-af-smeltetiden.jpg” link1=”https://elbogen.dk/dimensionering-teori/#Valg_af_sikring_til_OB”]Sådan dimensionere du en sikring [/su_read_also]

Beregning af sikring ud fra 1,6 faktoren

$I_{N,SL}=1,6*I_{N,TS}=1,6*25=40 [A]$

Beregning af sikring ud fra sammenligning af smeltekurve.

En anden måde er at sammenligne de to sikrings smeltekurver. Da der anvendes samme sikringsproducent (Jeg har valgt SIBA i dette tilfælde), vil der være selektivitet ved valg af en større sikring. Jeg har derfor valgt at gå efter 35 ampere sikring.

Valg: 3 stk. 35 A D02 sikringer

Kontrol: $35 [A]> 25 [A] \rightarrow OK$

Valg af stikledning

Stikledning skal dimensioneres udfra belastningen og eventuelle kortslutninger. Overstrømsbeskyttelses (OB) kan foretages både forud og bagud. Det betyder, at stikledning kan dimensioneres efter tarifsikringen (forsikring).

Kortslutningsbeskyttelses (KB) skal foretages af beskyttelsesudstyr, der er placeret før stikledningen – altså tættest for forsyningspunktet. Derved skal kortslutningsbeskyttelsen af stikledning foretages af sikring i kabelskabet. Samtidig skal spændingsfaldet ikke overstige 3% for hele installationen

Derved kan følgende sættes op:

OB: $I_{Z,SL}\geq I_{n,ts}$

KB: $K^2*S_{SL}^2 \geq I_{k,min}^2*t$

Spændingsfald: $\Delta U \leq 3 [\%]$

Oplægningsmetode

Stikledning føres i jord samt alene i isoleret væg. Kablet føres ved en maksimal temperatur på 20 grader i jorden og 35 grader i væggen.

Kabel i isoleret ydervæg: Oplægning nr. 3 (A1) i henhold til tabel A.52.3 i DS60364
Kabel i jord: Oplægning nr. 72 (D2) i henhold til tabel A.52.3 i DS60364

Korrektionsfaktor

Temperatur: Da der i henhold til B.52.2.2 i DS60364 ikke skal foretages korrektion af kabler direkte i jord, har denne en korrektionsfaktor på 1. Da reference værdien for andre installationer end i jord har en reference på 30 grader, er kt-faktor 0,94 ved anvendelse af XLPE kabler (Tabel B52.14).

Samlet fremføring: Da kablet er alene er ks=1.

$I_{Z,SL,min,jord}=\frac{I_{n,ts}}{k_t*k_s}=\frac{25}{1*1}=25 [A]$

$I_{Z,SL,min,væg}=\frac{I_{n,ts}}{k_t*k_s}=\frac{25}{0,94*1}=26,6 [A]$

Ud fra Tabel B.52.3 i DS60364 (XLPE kabler) er A1 den værste tænkelig scenarie. Derfor dimensioneres kablet efter det.

Valg: 4×4 mm2 kabel med en strømværdi på 35 A.

Kontrol: $35 [A] \geq 25 [A] \rightarrow OK$

Spændingsfald

Spændingsfalds må i følge tabel G52.1 (DS/HD 60364) maksimalt være 3% ved belysnings og 5% ved anden anvendelse. Grundet spændingsfaldet fra tavlen ud til forbrugerne, skal spændingsfaldet holdes mindst muligt i stikledningen. For at beregne spændingsfald, skal kablets resistans beregnes. Kablet er 30 meter langt. Ved boliginstallationer antages det, at faseforskydning er cosp=1. Derved forsvinder den reaktive del i spændingsfaldformlen. Jeg har dog, for en god ordens skyld, valg at medtage X-leder i formlen. Jeg anvender desuden den tilnærmet formel for spændingsfald.

[su_read_also pic1=”https://elbogen.dk/wp-content/uploads/2018/05/Intro-v3.jpg” link1=”https://elbogen.dk/spaendingsfaldet/”]Hvordan beregnes spændingsfald? Lær at forstå teorien ved spændingsfaldsberegning.[/su_read_also]

Kablets resistans og reaktans skal beregnes. Og her anvendes NKT kataloget og kablets resistans og reaktans aflæses til:

$r_{SL}=4,61 [\frac{\Omega}{km}]$ (tabel 13)

$x_{SL}=0,099[\frac{\Omega}{km}$ (tabel 17)

Herefter bregnes resistansen, reaktansen og spændingsfaldet:

$R_{SL}=\frac{r_{SL}}{1000}*l=\frac{4,62}{1000}*30=0,138 [\Omega]$

$X_{SL}=\frac{x_{SL}}{1000}*l=\frac{0,099}{1000}*30=0,003 [\Omega]$

$\Delta U_{SL}=I_B*(R_{SL}*cos\phi+X_{SL}*sin\phi)=23,69*(0,138*cos(0)+0,003*sin(0))=3,28 [V]$

Spændingsfald i procent:

$\Delta U_{SL\%}=\frac{\Delta U_{SL}}{U_f}*100=\frac{3,28}{230}*100=1,42 [\% ]$

Kontrol: $1,42 [\%] \geq 3 [\%] \rightarrow OK$

Beregning af kortslutningsstrømmene i tavlen og ved forsyningspunktet

Bestemmelse af min og maks kortslutningsstrømmene

For at få oplyst kortslutningsstrømmen i forsyningspunktet, skal man normalvis kontakte sit forsyningsselskab. Dog kan man i henhold til fællesregulativet 2017 afsnit 12.1 læse, at man som elinstallatør skal regne med en minimum kortslutningsstrøm foran stikledning på 5 gange stikledningssikringen, samt en maksimum kortslutningsstrøm på 16kA med cosp=0,3 =72 grader. Minimum kortslutningsstrømmen beregnes ud fra sikring på 35 A. Derfor er vores mindste kortslutningsstrøm følgende:

[su_read_also link1=”https://elbogen.dk/kortslutningsberegning/”]Lær at beregne kortslutningsstrømme i et elektrisk kredsløb[/su_read_also]

$I_{k,min,SL}=I_{n,SL}*5=35*=175 [A]$

$I_{k,max,SL}=16 [kA]$

Stikledningen er 30 meter lang, skal den største og mindste kortslutningsstrøm i tavlen beregnes.

R og X ledet blev beregnet tidligere, og ud fra det kan kablets impedans beregnes.

$\vec Z_{SL}=\vec R_{SL}+\vec X_{XL}=0,138\angle 0^{\circ}+0,003 \angle 90^{\circ}=0,138 [\Omega] \angle 1,25^{\circ}$

Beregning af nettets impedanser, hvor C er korrektionsfaktor fundet i DS60909-0-202 tabel 1

$Z_{N,max}=\frac{U_f*C_{min}}{2*I_{k,min,SL}}=\frac{230*0,95}{2*175}=0,624 [\Omega] \angle 72^{\circ}$

$Z_{N,min} = \frac{U_n*C_{Max}}{\sqrt{3}*I_{k,max,SL}}=\frac{400*1,1}{\sqrt{3}*16000}=0,016 [\Omega] \angle 72^{\circ}$

Herved kan de nye impedanser i tavlen beregnes

$\vec Z_{GT,max}=\vec Z_{SL}+\vec Z_{N,max}=(0,138 \angle 1,25)+(0,624\angle 72)=0,682 [\Omega] \angle 60,1^{\circ}$

$\vec Z_{GT,min}=\vec Z_{SL}+\vec Z_{N,min}=(0,138 \angle 1,25)+(0,016 \angle 72)=0,144 [\Omega] \angle 7,268^{\circ}$

Beregning af kortslutningsstrømmen

$I_{k,min,GT}=\frac{U_f*C_{min}}{2*Z_{GT,max}}=\frac{230*0,95}{2*0,682}=160 [A]$

$I_{k,max,GT}=\frac{U_n*C_{max}}{\sqrt{3}*Z_{GT,min}}=\frac{400*1,1}{\sqrt{3}*0,144}=1764,126 [A]$

Kortslutningsbeskyttelse

Beregning af kortslutningsbeskyttelse er ud fra smeltekurver, og er en beregning af den samlede energigennemslip. Følgende formel skal derfor være opfyldt.

$K^2*S^2\geq I_k_{min}^2*t$

K-faktor er en konstant, der findes i DS/HD 60364 tabel 43A, og S er ledernes tværsnit angivet i mm2. Herefter er det den kortslutningsstrøm, samt den tid, det tager at koble ud. Ved smeltesikringer, anvendes den mindste kortslutningsstrøm, da denne resulterer i den største energigennemslip.

I henhold til tabel 43A DS/HD 60364, kan kablets K-værdi aflæses til 143 ved kobber og XLPE isolering, som som blev valgt til dimensionering. Kablets tværsnit er 4mm2

$K^2*S^2=143^2*4^2=327.184 [A^2 s]$

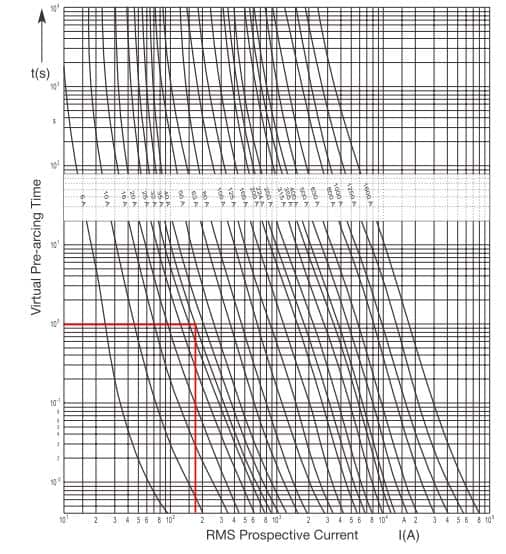
Ved aflæsning i SIBA smeltekurve for deres sikringer (Se efterfølgende billede), vil sikringen brænder over efter 1 sekund ved den mindste kortslutningsstrøm, der blevet beregnet før til 160 A ved gruppetavlen. Da udkoblingstiden er over 0,1 sekund, anvendes smeltekurven uden yderlig tilføjelser. Derved ser beregning ud som følgende:

$I^2*t=160^2*1=25.600 [A^2 s]$

Kontrol: $K^2*S^2\geq I_{k,min}^2*t \Leftrightarrow 327.184 \geq 25.600 [A^2 s] \rightarrow OK$

Smeltekurve (SIBA) — Smeltekurve fra SIBA sikringer. Lånt fra SIBA lavspændingssikringskatalog

Dimensionering af installationskablerne

Tidligere i indlægget blev automatsikringer valgt i størrelserne 10 og 16 A. Ud fra dette skal installationskablerne nu dimensioneres.

Krav:

$I_Z \geq I_n$ : OB
$K^2*S^2 \geq I_{k,max}^2*t=Q_{energi}$ : KB
$\Delta U \leq 3 [\%]$

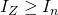OB af installationskablerne

Med 10 og 16 A sikringer valgt tidligere, beregnes installationen. Vi antager at kabler til huset er oplagt i isolerede vægge (Oplægningsmetode A1 i Tabel B.52.3 i DS/HD 60364), og at der maksimal er 4 kabel sammen (ks=0,65 i tabel B.52.17). Temperaturen er maks 20 grader (Kt = 1,08 i tabel B.52.14).

Kablet til udendørsbelysning er lagt alene i jord (Oplægningsmetode D2 i Tabel B.52.3 i DS/HD 60364). Kablet er dog oplagt 2 meter med de øvrige indendørs. Alle kabler er af typen XLPE.

Beregning

10A grupperne i huset: $I_{Z10}=\frac{I_n}{k_t*k_s}=\frac{10}{1,08*0,65}=14,25 [A]$

10A grupperne udendørs: $I_{Z10}=\frac{I_n}{k_t*k_s}=\frac{10}{1*1}=10[A]$

16A grupperne udendørs: $I_{Z16}=\frac{I_n}{k_t*k_s}=\frac{16}{1,08*0,65}=22,79 [A]$

Det værste scenarie for kablet til udendørsbelysning, er hvor kablet er oplagt med de øvrige indendørs. Derfor dimensioneres kablet ud fra dette. Ud fra Tabel B.52.3 oplægning A1 vælges 1,5 mm2 til 10 A grupperne med en strømværdi på 19 A. Til 16 A gruppen vælges en 2,5 mm2 med en strømværdi på 26 A.

Kontrol

10A $19 [A] \geq 14,25 [A]$

16A $26 [A] \geq 22,79 [A]$

KB af installationskablerne

Tidligere i indlægget blev automatsikringerne i størrelserne 10 og 16 A valgt. Ud fra dette skal installationskablerne nu dimensioneres. Her anvendes den tidligere beregnede maksimale kortslutningsstrøm i gruppetavlen (1764,126 A). Den anvendes til aflæsning af gennemløbsenergien i automatsikringerne, hvis kortslutning sker lige foran gruppeafbryderen. I diagrammet her under aflæses, den maksimale energigennemslip, der sker ved anvendelse af henholdsvis 10 og 16A.

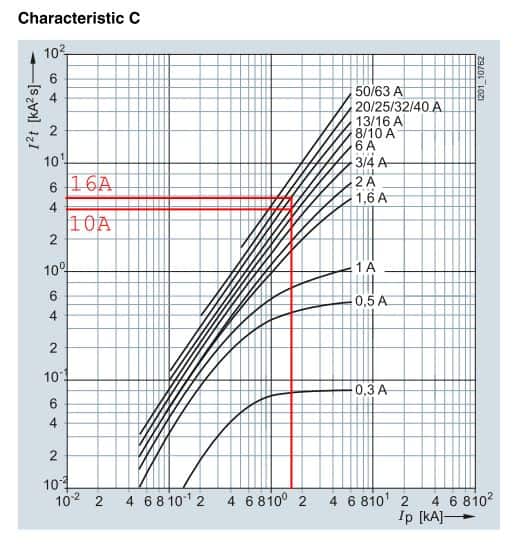
Energigennemslip Automatsikring — Billede fra Siemens katalog

Ud fra overstående diagram, aflæses gennemløbsenergi til ca. $3.900 A^2s$ ved 10A og $4.900 A^2s$ ved 16 A.

Igen ud fra K-faktoren i DS/HD 60364 tabel 43A på 143 kan følgende beregnes:

$143^2*1,5^2=46.010 [A^2s]$

$143^2*2,5^2=127.806 [A^2s]$

Kontrol

$46.010 \geq 3.900 \rightarrow OK!$

$127.806 \geq 4.900 \rightarrow OK!$

Spændingsfald

Lysgrupperne:

For at beregne spændingsfaldet skal belastningen kendes. Da belastningen på lysgrupperne er varierende, er det svært at fastlægge en maks belastning. Jeg antager at belastning på lysgrupperne ikke overstiger 80% af dens nominelle strøm. Vi tager vores worst-case scenarie, som er vores udendørsbelysning med en længde på 52 meter.

Beregning af impedansen i kablet til udendørs belysning:

I henhold til NKT katalog har vi en resistans på $12,10 \frac{\Omega}{km}$ (tabel 13) og en reaktans på $0,103 \frac{\Omega}{km}$ (tabel 17 3-leder)

$R_{LG5}=\frac{12,10}{1000}*52 =0,629 [\Omega]$

$X_{LG5}=\frac{0,103}{1000}*52 =0,005 [\Omega]$

Herved kan disse lægges sammen med resistans og reaktans i stikledning

$R_{tot}=R_{LG5}+R_{SL}=0,629+0,138=0,767 [\Omega]$

$X_{tot}=X_{LG5}+X_{XL}=0,005+0,003=0,008 [\Omega]$

Den samlede spændingsfald for lysgruppe 5 er.

$\Delta U_{LG5}=I_{B,80\%}*(R_{tot}*cos\phi+X_{tot}*sin\phi)=8*(0,767*cos(0)+0,008*sin(0))=6,136 [V]$

Spændingsfald i procent

$\Delta U_{LG5\%}=\frac{\Delta U_{LG5}}{U_f}*100=\frac{6,136}{230}*100=2,67 [\% ]$

Kontrol: $2,67 [\%] \geq 3 [\%] \rightarrow OK$

Kraftgrupperne:

Den mest belastede fase ved Kraftgruppe 1 er belastede med 16A og den mest belastede ved kraftgruppe 2 er belastet med 10A.

Kraftgruppe 1 med 2,5 mm2 kabel: I henhold til NKT katalog er resistansen på $7,41 \frac{\Omega}{km}$ (tabel 13) og en reaktans på $0,105 \frac{\Omega}{km}$ (tabel 17 5-leder)

$R_{KG1}=\frac{7,41}{1000}*20 =0,148 [\Omega]$

$X_{KG1}=\frac{0,105}{1000}*20 =0,002 [\Omega]$

Beregning af den samlede impedans

$R_{tot}=R_{KG1}+R_{SL}=0,148+0,138=0,286 [\Omega]$

$X_{tot}=X_{KG1}+X_{XL}=0,002+0,003=0,005 [\Omega]$

Den samlede spændingsfald for kraftgruppe 1 er.

$\Delta U_{KG1}=I_{B}*(R_{tot}*cos\phi+X_{tot}*sin\phi)=16*(0,286*cos(0)+0,005*sin(0))=4,576 [V]$

Spændingsfald i procent

$\Delta U_{KG1\%}=\frac{\Delta U_{KG1}}{U_f}*100=\frac{4,576}{230}*100=1,99 [\% ]$

Kontrol: $1,99 [\%] \geq 3 [\%] \rightarrow OK$

Kraftgruppe 2 ved 1,5 mm2 kabel: I henhold til NKT katalog er resistansen på $12,10 \frac{\Omega}{km}$ (tabel 13) og en reaktans på $0,113 \frac{\Omega}{km}$ (tabel 17 5-leder)

$R_{KG2}=\frac{12,10}{1000}*22 =0,266 [\Omega]$

$X_{KG2}=\frac{0,113}{1000}*22 =0,002 [\Omega]$

Beregning af den samlede impedans

$R_{tot}=R_{KG2}+R_{SL}=0,266+0,138=0,404 [\Omega]$

$X_{tot}=X_{KG2}+X_{XL}=0,002+0,003=0,005 [\Omega]$

Den samlede spændingsfald for kraftgruppe 2 er.

$\Delta U_{KG2}=I_{B}*(R_{tot}*cos\phi+X_{tot}*sin\phi)=10*(0,404*cos(0)+0,005*sin(0))=4,04 [V]$

Spændingsfald i procent

$\Delta U_{KG2\%}=\frac{\Delta U_{KG2}}{U_f}*100=\frac{4,04}{230}*100=1,76 [\% ]$

Kontrol: $1,76 [\%] \geq 3 [\%] \rightarrow OK$

Kontrol af automatsikringernes udkobling

Til sidst skal det kontrolleres at automatsikringerne kobles ud ved kortslutningsstrømmene. Den maksimal kortslutningsstrøm i gruppetavlen er beregnet tiltil 1764,126 A. Derved kan det kotrnolleres om automatsikringer kan koble ud ved den maksimale kortslutningsstrøm.

Kontrol: $6 [kA] \geq 1,76 [kA] \rightarrow OK$

Herefter skal den mindste kortslutningsstrøm kontrolleres. Af 10 A sikringer er udendørslyset den mest kritiske og, derfor beregner den. Resistansen og reaktansen blev tidligere beregnet for kablet.

$R_{LG5} =0,629 [\Omega]$

$X_{LG5} =0,005 [\Omega]$

Derved kan impedansen beregnes

$\vec Z_{LG5}=\vec R_{LG5}+\vec X_{LG5} =(0,629 \angle 0)+(0,005 \angle 90)=0,629 [\Omega] \angle 0,46^{\circ}$

Lægges impedanserne sammen med den tidligere beregnede, fås den samlede impedans i enden af kablet på.

$\vec Z_LG5,Max}=\vec Z_{LG5}+\vec Z_{GT,max}=(0,629 \angle 0,46)+(0,682 \angle 60,1)=1,138 [\Omega] \angle 31,61^{\circ}$

Derved kan den mindste kortslutningsstrøm beregnes (hvor C er korrektionsfaktor fundet i DS60909-0-202 tabel 1):

$I_{k,min,LG5}=\frac{U_f*C_min}{2*Z_LG5,Max}=\frac{230*0,95}{2*1,138}=96 [A]$

Kontrol

$100 [A] \leq 90 [A] \rightarrow FEJLET$

Da denne ikke er OK, skal det sikres, at kortslutningsniveauet øges. Derfor kan en mulighed være at øge kvadratet på stikledning til 6mm2. Ved udskiftning, skal det dog huskes at kontrollere, om IKmax bliver ændret i sådan en grad, at det får betydning for KB af installationskablerne, og kortslutningen overstiger 6kA, som automatsikringerne er monteret ved.

6 mm2 har en r på 3,080 $\frac{\Omega}{km}$ og 0,097 $\frac{\Omega}{km}$

$R_{SL6}=\frac{r_{SL6}}{1000}*l=\frac{3,080}{1000}*30=0,092 [\Omega]$

$X_{SL6}=\frac{z_{SL6}}{1000}*l=\frac{0,097}{1000}*30=0,003 [\Omega]$

$\vec Z_{SL6}=\vec R_{SL6}+ \vec R_{SL6}=(0,092 \angle 0)+(0,003 \angle 90)=0,092 [\Omega] \angle 1,87^{\circ}$

Den samlede impedans

$Z_{LG5,Max}=\vec Z_{LG5}+\vec Z_{SL6}+\vec Z_{N,max}$

$Z_{LG5,Max}=(0,629 \angle 0,46)+(0,092\angle 1,87)+(0,624\angle 72)=1,09 [\Omega] \angle 33,36^{\circ}$

Mindste kortslutning beregnes igen

$I_{k,min,LG5}=\frac{U_f*C_min}{2*Z_LG5,Max}=\frac{230*0,95}{2*1,09}=100,2 [A]$

Kontrol

$100 [A] \leq 100,2 [A] \rightarrow OK$

Og til sidst kontrol af 16A gruppen.

$R_{KG1} =0,148 [\Omega]$

$X_{KG1} =0,002 [\Omega]$

Derved kan impedansen beregnes

$\vec Z_{KG1}=\vec R_{KG1}+\vec X_{KG1} =(0,148 \angle 0)+(0,002 \angle 90)=0,148 [\Omega] \angle 0,77^{\circ}$

Lægges vores impedans sammen med den tidligere beregnede får vi en samlet impedans i enden af kablet på.

$Z_{KG1,Max}=\vec Z_{KG5}+\vec Z_{SL6}+\vec Z_{N,max}$

$Z_{KG1,Max}=(0,148 \angle 0,77)+(0,092\angle 1,87)+(0,624\angle 72)=0,739 [\Omega] \angle 54,13^{\circ}$

Derved kan den mindste kortslutningsstrøm beregnes (hvor C er korrektionsfaktor fundet i DS60909-0-202 tabel 1):

$I_{k,min,KG1}=\frac{U_f*C_min}{2*Z_KG1,Max}=\frac{230*0,95}{2*0,739}=147,83 [A]$

Kontrol

$160 [A] \leq 147,83 \rightarrow FEJLET$

Overstående eksempel er igen fejlet. Derfor kan man vælge at gå endnu et kvadrat op, eller man kan vælge en anden type automatsikring eksempelvis type B.

Claus Hansen

Claus Hansen har med sin uddannelse som elektriker og maskinmester stor viden inden for elteorien og elinstallationer. Han ønsker med Elbogen.dk at vejlede og hjælpe studerende, private og folk i branchen med love, regler og teorien. Har du spørgsmål? Så send ham endelig en besked via kontaktformularen, der findes i de forskellige indlæg eller under kontakt i menuen.

Følge os på Facebook og bliv opdateret på de nyeste indlæg

Spørgsmål? Så send dem til mig

Kontakt mig her!